
However, the problem of quantum oscillator with time-varying frequency had been solved.
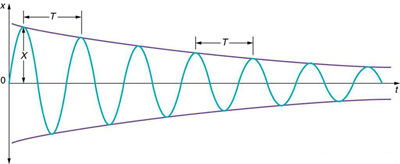
The damping is here considered in the form of Caldirola-Kanai Model and the recently developed model. The aim of this paper is to evaluate the damped harmonic mechanical oscillator.

Recently, Tarasov has evaluated the quantization and classical distribution for dissipative systems. The CK, on one hand, is an open system whose parameters such as mass and frequency are all time dependent ,and, on the other hand, the BFT is a closed system whose total energy is conserved and the dissipated energy from the damped oscillator is transferred to amplified. Another representation is the Bateman-Feshbach-Tikochinsky (BFT) oscillator, which consists of a damped and an amplified oscillator. One representation of the damped system is the Caldirola-kanai (CK) oscillator which is a one-dimensional system with an exponentially increasing mass. In the canonical approach, two different Hamiltonian representations have been introduced for these damped oscillators. The simplest model for dissipation is damped oscillators with one or two degrees of freedom. There have been attempts to understand dissipation at a more fundamental level. Dissipation is usually ascribed as having a microscopic nature.

The quantum theory is, however, governed by the Schrödinger equation whereas classical theory is governed by the Hamilton equation, for instance. Quantum effects usually manifested themselves at the microscopic level. Quantum theory has been shown to be the fundamental law of nature and presently is the most correct theory of all microscopic and macroscopic systems. We also investigate the cases of under-, over-, and critical damping. The exact solutions of the Schrödinger equation for quantum damped oscillator with modified Caldirola-Kanai Hamiltonian are evaluated.


 0 kommentar(er)
0 kommentar(er)
